计组笔记_chapter2

IEEE浮点表示

规格化表示：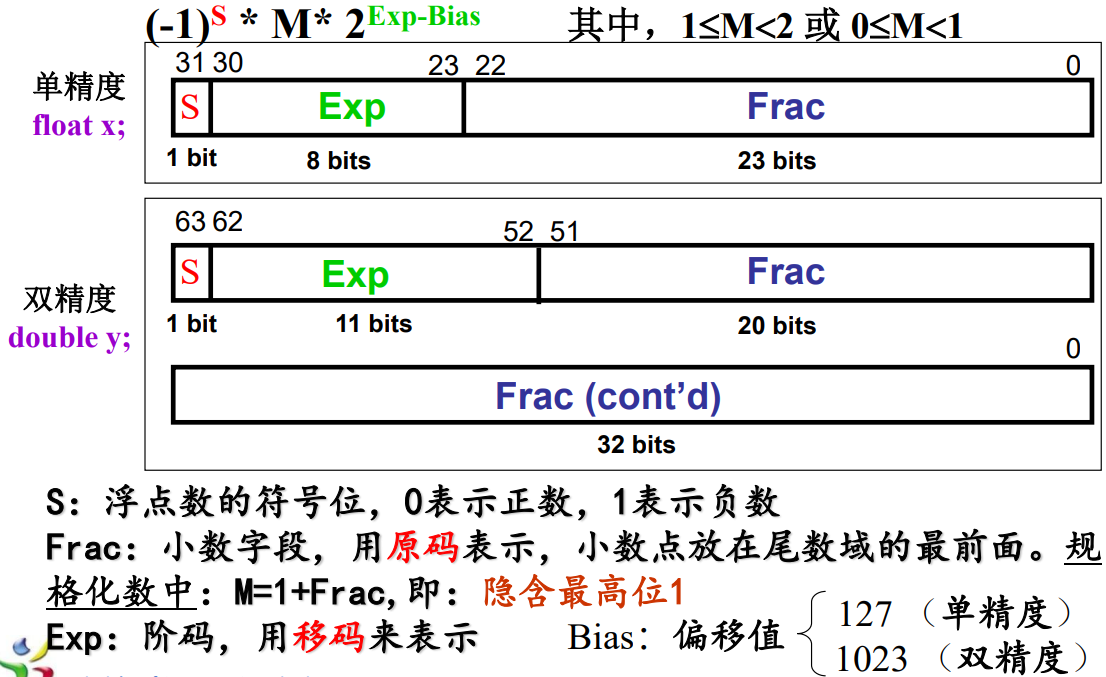

特殊的浮点数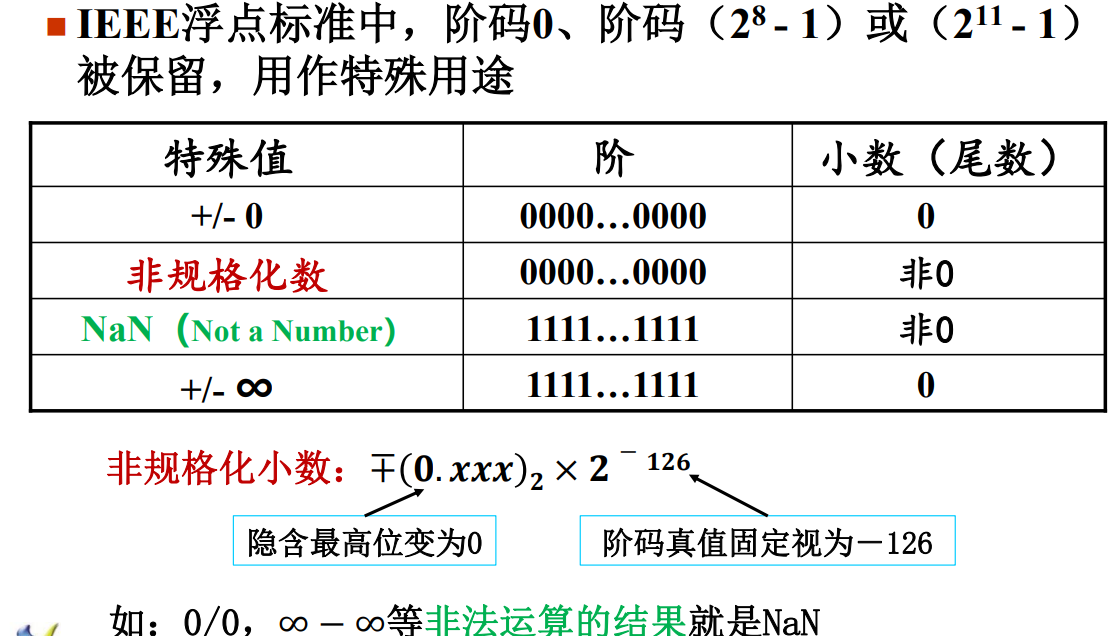

浮点数表示的范围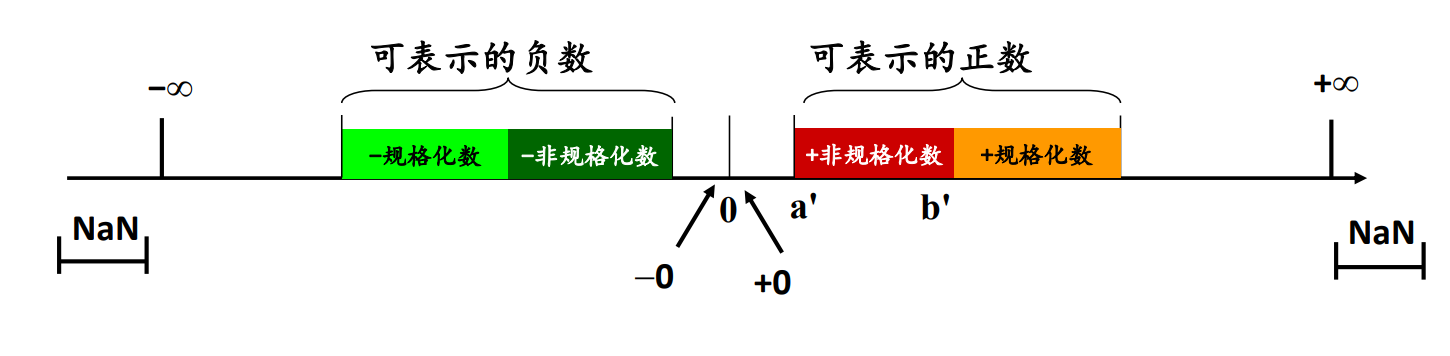

小结：
对32位浮点数N：
◼ 若0 < E < 255，则
N ＝ (-1)s ×1.M ×2
E-127 ，规格化数表示
◼ 若E = 0且M ＝ 0，则
N ＝ (-1)s 0，机器+0、-0表示
◼ 若E = 0且M ≠ 0，则
N ＝ (-1)s × 0.M× 2
1-127 ，非规格化数表示
◼ 若E= 255且M ＝ 0，则
N＝(-1)s∞（正无穷大，负无穷大）
◼ 若E = 255且M ≠ 0，则
N ＝ NaN，非数NaN(Not a Number)

十进制小数转二进制：
十进制的小数转换为二进制，主要是小数部分乘以2，取整数部分依次从左往右放在小数点后，直至小数点后为0。

ACSII码

数字：48（0011 0000）~ 57（0011 1001） +10-1
大写字母：65（0100 0001）～90（0101 1010） +26-1
小写字母：97（0110 0001）～122（0111 1010） +26-1

存储器中的字节序

每个字节内部的顺序都是固定的，仅需考虑多个字节的字节间关系

• 小端方式Little Endian
  • 低字节存放在小地址处，即低字节在前高字节后
    x86处理器
• 大端方式Big Endian
  • 低字节存放在大地址处，即高字节在前低字节后
    SPARC处理器，IBM Power处理器

补码

溢出

整数溢出

正溢：运算结果为正，且超出机器所能表示的范围
负溢：运算结果为负，且超出机器所能表示的范围

小数溢出

上溢：结果的绝对值大于机器所能表示的最大绝对值（+∞，－∞）
（overflow）
下溢：结果的绝对值小于机器所能表示的最小绝对值 （ 机器零 ）
（underflow）

检测方法

1. 双符号位法，又称变形补码，或者模四补码
   双符号位的补码也遵循加法法则。
   在计算中：
   两个符号位均参加运算
   最高符号位上产生的进位要丢掉

   溢出检测规则：
   ◆两数相加后，结果的符号位出现“01”或“10”两种情况时，表示发生溢出（也就是最高的两位异或）
   ◆最高符号位永远表示结果的正确符号

2. 单符号位法
   溢出的逻辑表达式为
   $V=C_f⊕C_0$
   $C_f$为符号位产生的进位，$C_0$为最高有效位产生的进位

定点乘法运算算法

原码一位乘法运算

无符号的阵列乘法

有符号的阵列乘法

补码一位乘法运算（不要求）
原码两位乘法运算（不要求）
直接补码并行乘法（不要求）