形式语言与自动机_4
第四章 上下文无关文法与下推自动机
上下文无关文法:CFG(contex free grammar)
2型文法,产生式形如A->a,A$\in$N
对应的识别器:下推自动机
PDA(push down Automata)
PDA由输入带,有限控制器和下推栈组成
归约和推导
推理字符串是否属于文法所定义的语言
- 一种是自下而上的方法,称为递归推理(recursive inference),递归推理的过程习称为归约;
- 一种是自上而下的方法,称为推导(derivation).
- 归约过程 将产生式的右部(body)替换为产生式的左部( head ).
- 推导过程 将产生式的左部( head )替换为产生式的右部( body )
例子:

- 最左推导(leftmost derivations)
若推导过程的每一步总是替换出现在最左边的非终结符。
- 最右推导(rightmost derivations)
若推导过程的每一步总是替换出现在最右边的非终结符。
推导树和文法的二义性
推导树
用图的方法表示一个句型的推导,这种图称为推导树(也称语法树或语法分析树)
文法的起始符为根,树的枝结点标记是非终结符,叶结点标记为终结符或$\sigma$。
若枝结点有直接子孙x1, x2,…, xk,则文法中有生成式A→x1x2…xk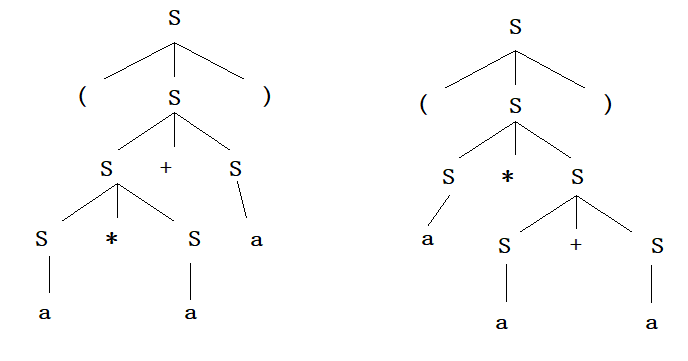

推导树是对文法G中一个特定句子形式的派生过程所做的一种自然描述。
- 边缘
叶子从左向右组成的字符串称为推导树的边缘。
归约、推导与分析树之间关系
归约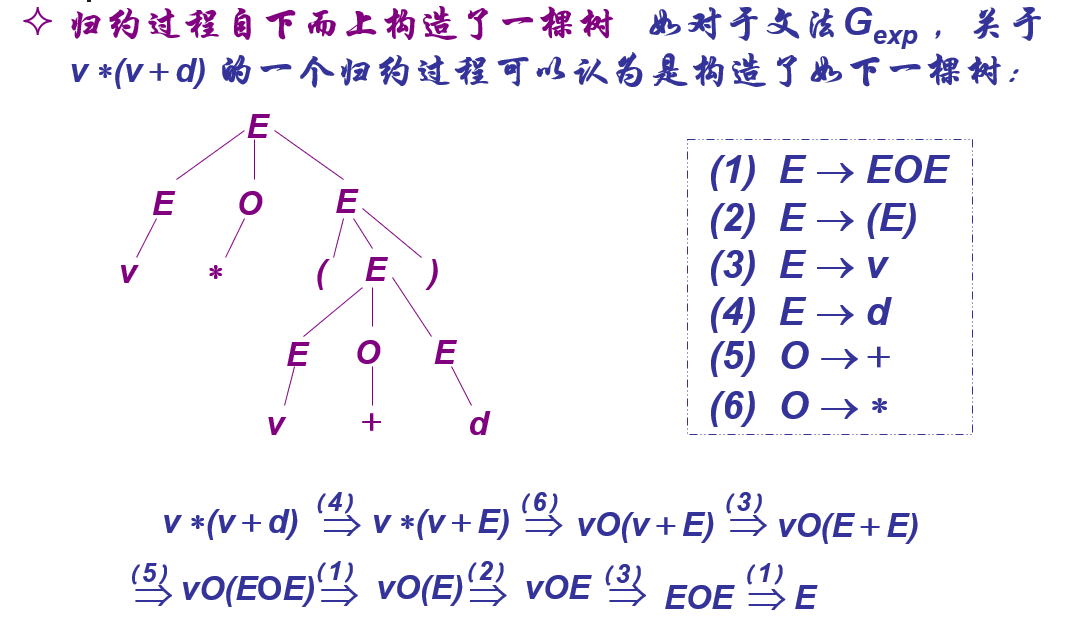
推导
关系
证明2->5:
设2型文法G=(N,T,P,S),如果存在S ω,当且仅当文法G中有一棵边缘为ω的推导树。
ω,当且仅当文法G中有一棵边缘为ω的推导树。
二义性
2型文法是二义的,当且仅当对于句子ω∈L(G),存在两棵不同的具有边缘为ω的推导树。
(即:如果文法是二义的, 那么它所产生的某个句子必然能从不同的最左(右)推导推出)。
- 可有二个文法,一个有二义,一个无二义,但产生相同的语言.
- 可否通过变换消除二义性? —— 无一般的算法!
上下文无关文法的变换
- CFG 的简化
- 消无用符号
- 消$\varepsilon$产生式
- 消单产生式
- 对生成式形式进行标准化
生成式的标准形式:
- Chomsky范式 :
CNF - Chomsky Normal Form

- Greibach范式:(GNF)

消去无用符号
有用符号X

- 生成符号 generating symbol

- 可达符号 reachable symbol
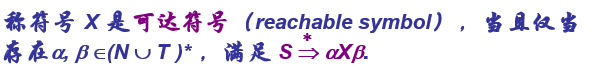
无用符号
- 非生成符号
- 不可达符号
消去无用符号的步骤
- 计算生成符号集
- 计算可达符号集
- 消去非生成符号、不可达符号
- 消去相关产生式
计算生成符号
思路
算法1:找出有用非终结符
算法1图示: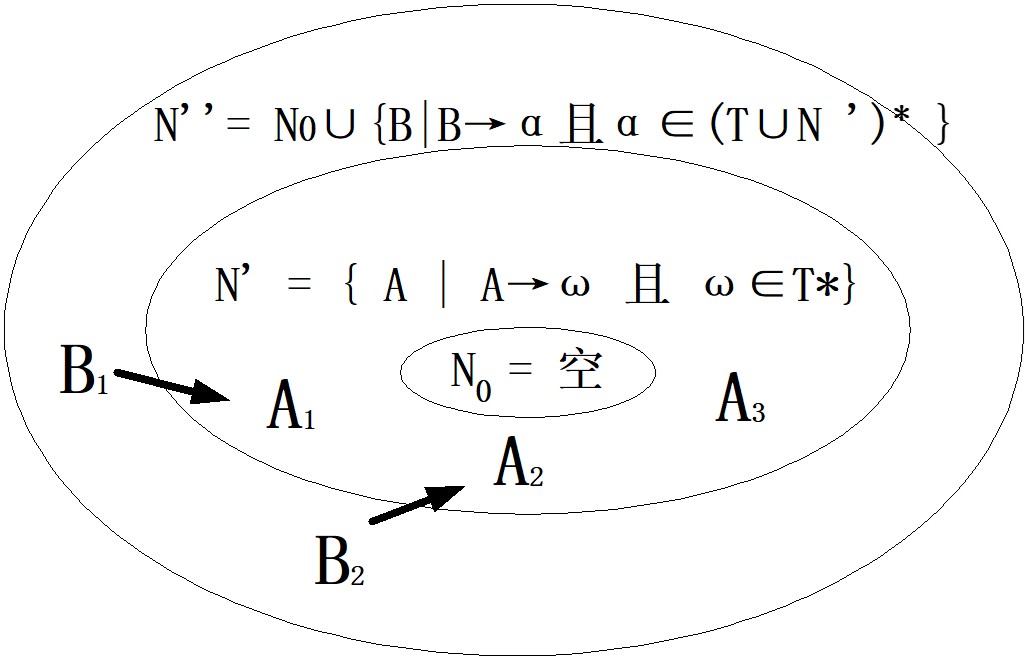
一层层向外扩展,直至最外两层相等为止。所得集合即是算法1的有用符号。
计算可达符号集
思路
算法2:找出有用符号(从S出发可达的符号)
图示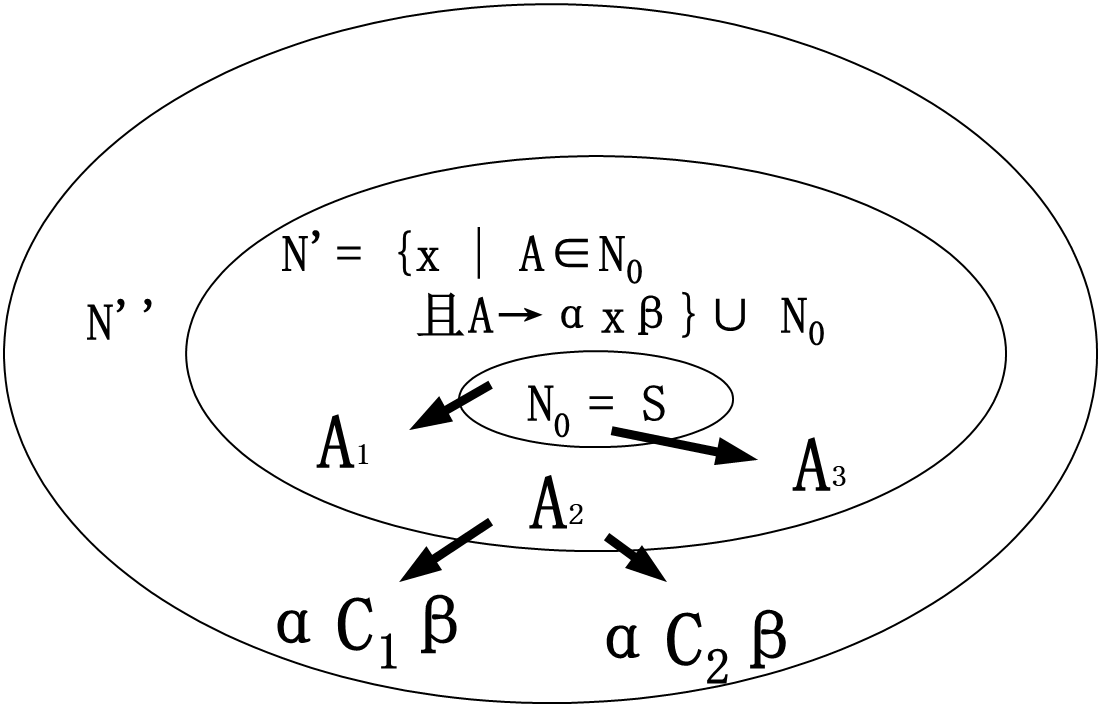
一个例子

注意:在删除一个无用符号时,要把与它相关的式子也删掉。
并且,一定要先执行算法1,保证每个符号是生成符号,再执行算法2,保证每个符号是可达符号。否则可能会导致一些无用符号无法消除。(这个例子就是不这么干的反例)
一个定理:
任何非空的上下文无关语言,可由不存在无用符号的上下文无关语言产生(证明略)
消去$\varepsilon$产生式
目的:方便文法的设计, 利于文法规范化.
影响:消去$\varepsilon$产生式, 除了文法不能产生字符串$\varepsilon$外,不会影响到原文法相应的语言中其它字符串的产生.
可致空符号
nullable symbol
算法3: 生成无$\varepsilon$文法
定义:若G的生成式中无任何$\varepsilon$产生式,或只有一个生成式S→$\varepsilon$且S不出现在任何生成式的右边,则称G为无$\varepsilon$文法。
思路:
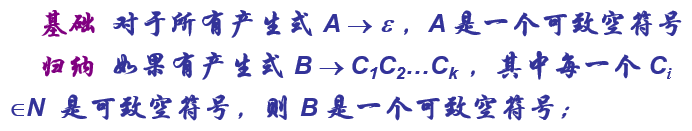
算法步骤


例子:
消去单产生式
什么是单产生式
单产生式 形如 A->B 的产生式,其中A、B 为非终结符.
目的:
可简化某些证明,减少推导步数, 利于文法规范化.
单元偶对 unit pairs

消去单产生式的算法
思路

算法步骤

$N_A$可以理解成所有和A是单元偶对的非终结符的集合
例子



小结

注意 以上简化步骤的次序.
设 CFG G 的语言至少包含一个非 的字符串,通过上述步骤从 G 构造 G1 ,则有 L(G1)= L(G) - {$\varepsilon$}.
必须按照顺序的原因:
消去空生成式的时候,可能会引入一些单生成式,而消除单生成式的时候又可能引入一些无用符号。
消除递归
递归定义:
生成式的代换
引理1:
一个小例子: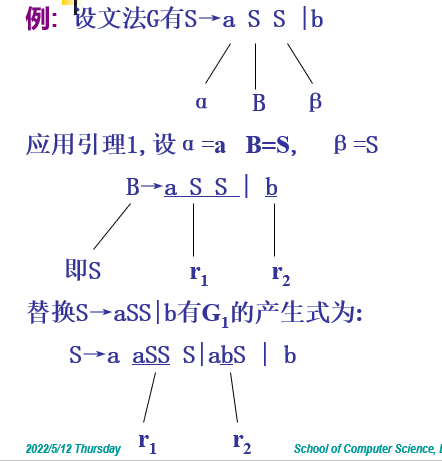
消除直接左递归
引理2
例子:
为什么要消除左递归?
- 以后的句法分析算法不适用于左递归,会引起死循环。
- 对于给定的2型文法, 该文法不存在无用符号, 无循环且是无ε生成式的文法, 为了消除G中可能存在的左递归, 构成一个等效的无左递归的文法G1, 可用算法5。
- 算法5在原理上与求解正规表达式方程组的算法类似.
算法5
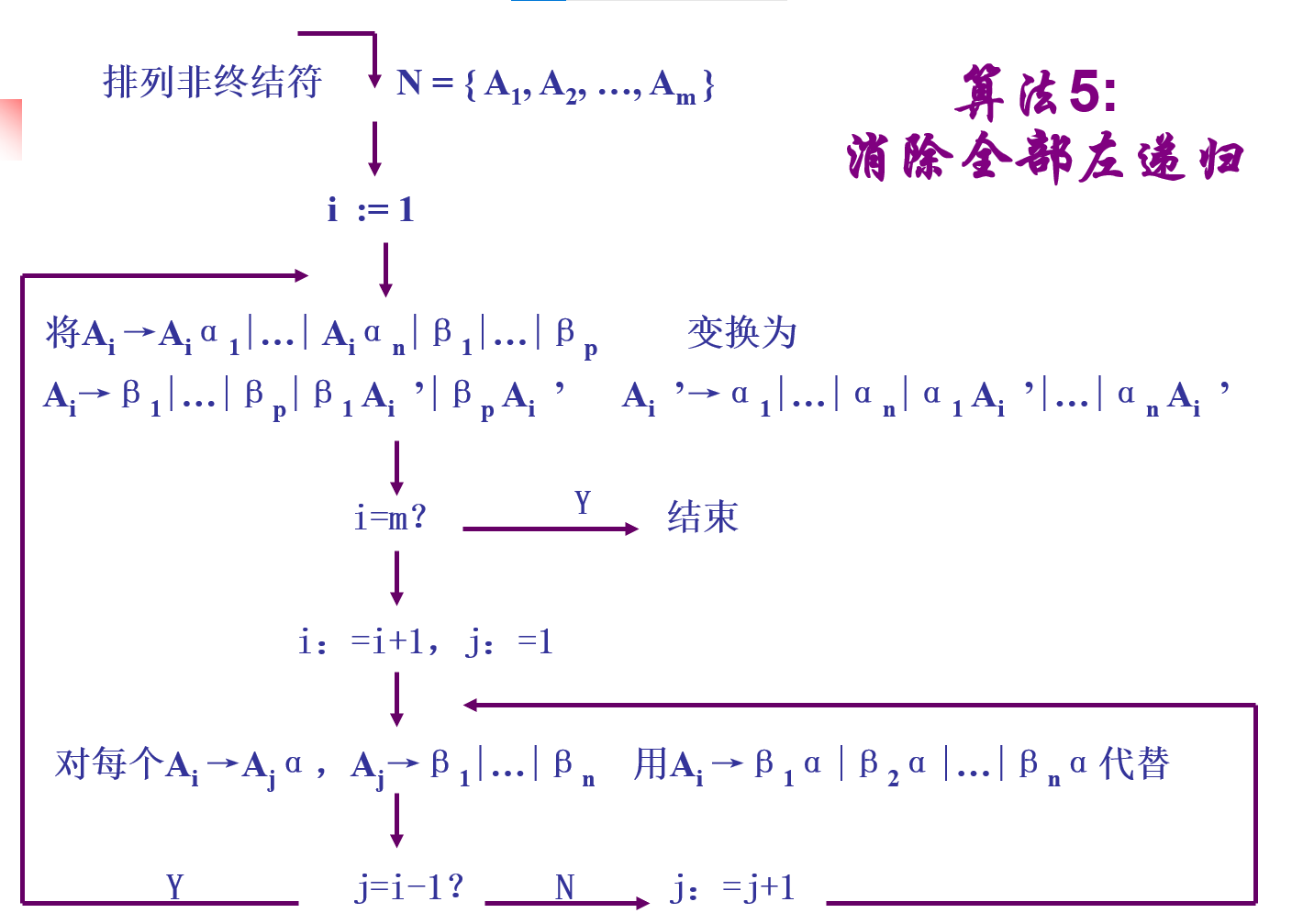
示例


下推自动机
上下文无关语言的性质
Chomsky范式和Greibach范式
Chomsky 范式
2型文法G=(N,T,P,S)
生成式形如:
A→BC和A→a
称为Chomsky Normal Format
特别的,若ε∈L(G),则S→ε是P的一个生成式,但S不能在任何其它生成式的右边
构成步骤:
- 消除ε生成式、无用符号、单生成式
- 引入新的非终结符,凑

Greibach范式
2型文法G=(N,T,P,S)
若生成式的形式都是A→aβ,A∈N,a∈T,β∈N*
且G不含ε生成式,则称G为Greibach范式,记为GNF
构成步骤:
- 2型文法变换为CNF。(A→a,A→BC形式)
- 对非终结符排序
- 假如按下标递增,不能出现$A1->A2\beta$(A2高于A1)
- 把A2的生成式带入,直至满足上述条件
- 消除左递归(只对最高的Ai进行消除左递归,消除完了之后Ai就会满足GNF形式,即终结符a开头,但会引入新的非终结符Ai’,这些新的非终结符优先级是最低的)
- 回代
- 依次回代Ai到Ai-1,Ai-1到Ai-2….一直到右部首字符都为终结符
- 将消除左递归时候引入的带’的右部进行代换,换成右部首字符都为终结符。
GNF1:
GNF2:
GNF3: